Question

An artificial satellite circles the Earth in a circular orbit at a location where the acceleration due to gravity is 6.03 m/s^2. Determine the orbital period of the satellite.

Answer 1

Orbital period, T = 2.02 hours

Step-by-step explanation:

It is given that, an artificial satellite circles the Earth in a circular orbit at a location where the acceleration due to gravity is 6.03 m/s². We have to find the orbital period (T) of the satellite.

Firstly, calculating the distance between Earth and satellite. The acceleration due to gravity is given by :

`a=(GM)/(r^2)`

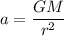
G = universal gravitational constant

M = mass of earth

`r=\sqrt{(GM)/(a)}`

`r=\sqrt{(6.67* 10^(-11)* 5.97* 10^(24))/(6.03\ m/s^2)}`

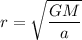
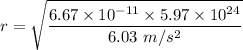
r = 8126273.3 m..........(1)

Now, according to Kepler's third law :

`T^2=(4\pi^2)/(GM)r^3`

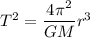
Putting the value of r from equation (1) in above equation as :

`T^2=(4\pi^2)/(6.67* 10^(-11)* 5.97* 10^(24))* (8126273.3)^3`

`T^2=53202721.01\ s`

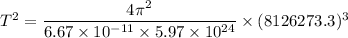
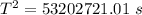
T = 7294.01 seconds

Since, 1 hour = 3600 seconds

Converting seconds to hour we get :

So, T = 2.02 hour

So, the orbital period of the satellite is 2.02 hours.