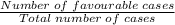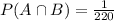Answer:
a. The two events are dependent.
b.
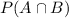 =
=
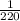 .
.
Explanation:
Given
Total coins =220
Number of Indian pennies= 6
A: When one of the 220 coins is randomly selected, it is one of the Indian pennies.
Therefore , the probability of getting an Indian pennies=
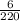
By using formula of probability=

Probability of getting an Indian pennies=
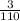
B: When another one of the 220 coins is randomly selected( with replacement) , It is also one of the Indian pennies.
Therefore, probability of getting an Indian pennies=
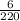
Probability of getting an Indian pennies =
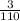
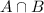 : 1
: 1
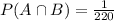
If two events are independent. Then
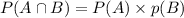
P(A).P(B)=
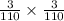 =
=
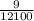
Hence,
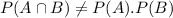
Therefore, the two events are dependent.
b. Probability that events A and B both occur
Number of favourable cases when both events A and B occur=1
Total coins=220
Probability=