Answer:
Part 1) The quadratic equation is

Part 2) The length of rectangle is 10 in and the width is 5 in
Explanation:
Part 1)
Find the quadratic equation
Let
x -----> the length of rectangle
y ----> the width of rectangle
we know that
The area of rectangle is equal to
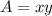
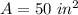
so
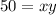 -----> equation A
-----> equation A
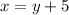
 -----> equation B
-----> equation B
substitute equation B in equation A
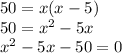
Part 2) Find the length of the rectangle

Solve the quadratic equation by graphing
The solution is

see the attached figure
Find the value of y
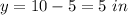
therefore
The length of rectangle is 10 in and the width is 5 in