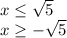What is the solution set of the quadratic inequality x^2-5< or equal to 0

Question

asked Jul 3, 2020 197k views

2 Answers

Stratedge · Answer 1 · 2020-07-08T11:04:50+0000

For this case we must indicate the solution of the following inequality:

$x ^ 2-5 \leq0$

Adding 5 to both sides of the inequality:

$x ^ 2\leq5$

We apply square root on both sides of the inequality to eliminate the exponent:

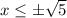
$x \leq\pm \sqrt {5}$

So, we have two solutions:

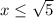
$x\leq \sqrt {5}$

Since it is an inequality, the sign for the negative portion is changed:

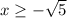
$x\geq- \sqrt {5}$

Answer:

$x\leq \sqrt {5}\\x\geq-\sqrt {5}$