Question

A wheel rotates without friction about a stationary horizontal axis at the center of the wheel. A constant tangential force equal to 82.0 N is applied to the rim of the wheel. The wheel has radius 0.150 m . Starting from rest, the wheel has an angular speed of 12.8 rev/s after 3.88 s. What is the moment of inertia of the wheel?

Answer 1

0.593 kg-m²

Step-by-step explanation:

edg.

Answer 2

The moment of inertia of the wheel is 0.593 kg-m².

Step-by-step explanation:

Given that,

Force = 82.0 N

Radius r = 0.150 m

Angular speed = 12.8 rev/s

Time = 3.88 s

We need to calculate the torque

Using formula of torque

`\tau=F* r`

`\tau=82.0*0.150`

`\tau=12.3\ N-m`

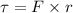
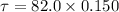
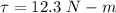
Now, The angular acceleration

`(d\omega)/(dt)=(12.8*2\pi)/(3.88)`

`(d\omega)/(dt)=20.73\ rad/s^2`

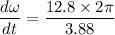
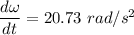
We need to calculate the moment of inertia

Using relation between torque and moment of inertia

`\tau=I*(d\omega)/(dt)`

`I=(I)/((d\omega)/(dt))`

`I=(12.3)/(20.73)`

`I= 0.593\ kg-m^2`

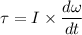
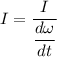
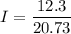
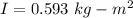
Hence, The moment of inertia of the wheel is 0.593 kg-m².