Answer:
Part 1) The inequality that describes the relationship between the number of cookies each one of them has is
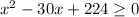
Part 2) Jessica has at least 2 cookies more than Martha
Explanation:
Part 1) Find the inequality that describes the relationship between the number of cookies each one of them has
Let
x----> the number of cookies when Jessica started
30-x ----> the number of cookies when Martha started
we know that
Each of them ate 6 cookies from their bag
so
The cookies left in each bag are
(x-6) ----> Jessica
and (30-x-6)=(24-x) ---> Martha
The product is equal to (x-6)(24-x)
The product of the number of cookies left in each bag is not more than 80.
so
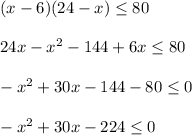
Multiply by -1 both sides
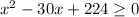
Part 2) Solve the quadratic equation
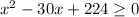
Solve by graphing
The solution is x=16 cookies
so
(30-x)=30-16=14 cookies
therefore
The number of cookies when Jessica started was 16 cookies
The number of cookies when Martha started was 14 cookies
The number of cookies left in each bag is equal to
Jessica
16-6=10 cookies
Martha
14-6=8 cookies
Jessica has at least 2 cookies more than Martha