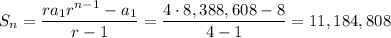Question

Find the sum of the following series. Round to the nearest hundredth if necessary.

Answer 1

11,184,808

Explanation:

The n-th term of a geometric series is ...

an = a1·r^(n-1)

To fill in the formula, we need a1·r^n, so need to multiply the last term shown by r.

The value of r is 32/8 = 4, and the other terms of interest are a1 = 8, a1·r^(n-1) = 8388608. So, the sum is ...

`S_n=(ra_1r^(n-1)-a_1)/(r-1)=(4\cdot 8,388,608-8)/(4-1)=11,184,808`