Question

Tori examined the pattern of exponents in the table.

Based on the pattern, which statements are true? Check all that apply.

Answer 1

Answer: The correct options are

(B) the value of b is
`(1)/(36).`

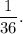
(C) As the value of the exponent decreases, each previous value is divided by 6.

Step-by-step explanation: We are given that Tori examined the pattern of exponents in the following table :

`\textup{power of 6}~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\textup{value}\\\\6^3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~216\\\\6^2~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~36\\\\6^1~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~6\\\\6^0~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~1\\\\6^(-1)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~a\\\\6^(-2)~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~b`

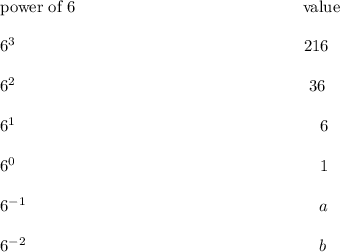
We are to select the true statements based on the above pattern.

We will be using the following property of exponents :

`x^(-y)=(1)/(x^y).`

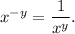
Therefore, we get

`a=6^(-1)=(1)/(6^1)=(1)/(6).`

and

`b=6^(-2)=(1)/(6^2)=(1)/(36).`

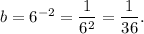
Also, the value of the exponent is decreasing and we see that

`(216)/(36)=(36)/(6)=(6)/(1)=(1)/((1)/(6))=((1)/(6))/((1)/(36))=6.`

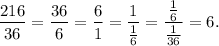
So, each previous value is divided by 6.

Thus, the correct options are

(B) the value of b is
`(1)/(36).`

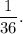
(C) As the value of the exponent decreases, each previous value is divided by 6.

Answer 2

Option B and C are correct.

Explanation:

We need to find the pattern of the values in the table and find the values of a and b.

6³ = 216

216/6 = 36

6² = 36

36/6 = 6

6¹ = 6

6/6 = 1

6⁰ = 1

1/6 = 1/6

6⁻¹ = 1/6

1/6*1/6 = 1/36

6⁻² = 1/36

So, value of a = 1/6

and value of b = 1/36

And we have seen as the exponent is decreasing, each previous value is divided by 6.

So, Option B and C are correct.