Question

Solution set of 2x + y < 4

Answer 1

Explanation:

Subtract

2

x

from both sides of the equation.

y

=

4

−

2

x

x

−

y

=

2

Subtract

x

from both sides of the equation.

y

=

4

−

2

x

−

y

=

2

−

x

Multiply each term in

−

y

=

2

−

x

by

−

1

Tap for more steps...

y

=

4

−

2

x

y

=

−

2

+

x

Create a graph to locate the intersection of the equations. The intersection of the system of equations is the solution.

(

2

,

0

)

Answer 2

See attachment

EXPLANATION

The given inequality is

`2x + y \: < \: 4`

To solve we need to graph this inequality.

To do that we graph the corresponding linear equation

`y = - 2x + 4`

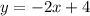
This is a straight line with slope

`m = - 4`

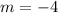
and y-intercept (0,4)

The graph of this function is to the right of the origin.

The solution set of the corresponding inequality is the half plane that is shaded.

We plot the point (0,0) into the given inequality to determine which half plane must be shaded

`2(0) + 0 \: < \: 4`

`0 < 2`

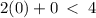
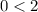
This is true so we shade the lower half plane. The solution set is the lower half plane shaded in the attachment.

Note that the boundary line must be a dashed line because the inequality does not involve equal sign.