Question

Which of the following best describes the graph below?

A. It is a function, but it is not one-to-one.
B. It is a one-to-one function.
C. It is not a function.
D. It is a many-to-one function.

Answer 1

B. It is a one to one function.

Explanation:

It is a function, if we trace the vertical line
`x=a` it intersects exactly one point of the graph (in the case that
`a\\eq0`.Moreover, the line
`x=0` doesn't intersects the graph, hence the given graph is the graph of a function with domain
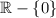`\mathbb{R}-\{0\}`. On the other hand, a function f(x) is one to one, if whenever f(x)=f(y) it holds that x=y, in terms of the graph of a function this mean that whenever we trace a vertical line
`y=b` it intersects exactly one point, which is exactly the case fo our given graph. Threfore, it is the graph of a one to one function

Answer 2

B. It is a one-to-one function.

Explanation:

Each value of the domain maps to a unique value of the range. It is a one-to-one function.