Answer:
the equation is true only if c=6 and d=2.
Explanation:
We have the following expression:
![\sqrt[3]{162x^(c)y^(5)} = 3x^(2)y\sqrt[3]{6y^(d)}](https://img.qammunity.org/2020/formulas/mathematics/college/zuywhd746ie0pypnkjbihw9mvqjv990d3i.png)
Elevating to the power of three:
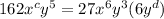
Simplifying:
→
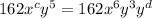
→
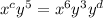
→

By comparing the two expression, we can say that:
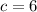
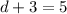 →
→
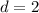
Therefore, the equation is true only if c=6 and d=2.