Question

The contents of 3838 cans of Coke have a mean of x¯¯¯=12.15x¯=12.15. Assume the contents of cans of Coke have a normal distribution with standard deviation of σ=0.12.σ=0.12. Find the value of the test statistic zz for the claim that the population mean is μ=12.μ=12.

Answer 1

Answer: 7.7055

Explanation:

Given: Sample size :
`n= 38> 30\text{ i.e. Large sample}`

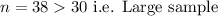
Sample Mean :
`\overline{x}=12.15`

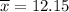
Standard deviation :
`\sigma =0.12`

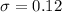
Claim : The population mean is
`\mu=12`

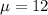
We assume the contents of cans of Coke have a normal distribution .

We know that the test-static for population mean for larger sample is given by :-

`z=\frac{\overline{x}-\mu}{(\sigma)/(√(n))}`

`\Rightarrow z=(12.15-12)/((0.12)/(√(38)))=7.70551750371\approx7.7055`

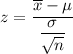
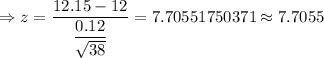
Hence, the value of the test statistic z for the claim that the population mean is μ=12 is 7.7055.