Answer: The correct option is
(B) 2x = 14.
Step-by-step explanation: We are given to solve the following system of equations by the method of Elimination :

Also, to select the resulting equation when we eliminate y.
Adding equations (i) and (ii), we get
![(x+y-6)+(x-y-8)=0+0\\\\\Rightarrow 2x-14=0\\\\\Rightarrow 2x=14~~~~~~~~~~[\textup{this is the resulting equation}]\\\\\Rightarrow x=(14)/(2)\\\\\Rightarrow x=7.](https://img.qammunity.org/2020/formulas/mathematics/middle-school/z9a5qkr9s4qmlvnx4y668tg95dopncgwm1.png)
From equation (i), we get
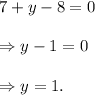
Thus, the required solution is (x, y) = (-1, 7) and the resulting equation while eliminating y is 2x = 14.
Option (B) is CORRECT.