Question

Which of the following represents the zeros of f(x) = 6x3 − 31x2 + 4x + 5?

−5, one third , one half

5, − one third , one half

5, one third , − one half

5, one third , one half

Answer 1

Answer: The correct option is

(B) 5, − one third , one half.

Step-by-step explanation: We are given to select the correct option that represents the zeroes of the following cubic function :

`f(x)=6x^3-31x^2+4x+5~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that

if for any number a, the function f(x) is zero at x =a , then x = a is a zero of the function f(x).

We have, for the given function, at x = 5,

`f(5)\\\\=6*5^3-31*5^2+4*5+5\\\\=125*6-31*25+20+5\\\\=750-775+25\\\\=0`

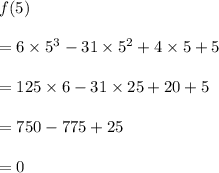
So, x = 5 is a zero of the function f(x).

Now, we have

`f(x)\\\\\=6x^3-31x^2+4x+5\\\\=6x^2(x-5)-x(x-5)-(x-5)\\\\=(x-5)(6x^2-x-1)\\\\=(x-5)(6x^2-3x+2x-1)\\\\=(x-5)(3x(2x-1)+1(2x-1))\\\\=(x-5)(3x+1)(2x-1)`

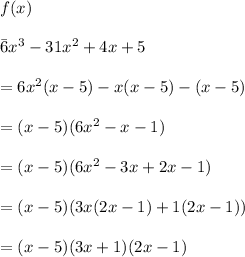
The zeroes of f(x) are given by

`f(x)=0\\\\\Rightarrow (x-5)(3x+1)(2x-1)=0\\\\\Rightarrow x-5=0,~~3x+1=0,~~2x-1=0\\\\\Rightarrow x=5,-(1)/(3),(1)/(2).`

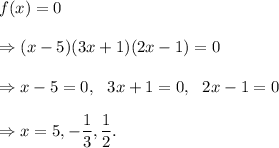
Thus, the zeroes of f(x) are 5, -one-third, one half.

Option (B) is CORRECT.

Answer 2

5, − one third , one half

Explanation:

If the number 'n' is a zero of f(x), then f(n)=0.

We could solve this problem by factorizing the polynomial, but the quickest way is by plugging the options into the equation.

We know that f(x) = 6x3 − 31x2 + 4x + 5.

Then:

• f(-5) ≠ 0

• f(1/3) ≠ 0

• f(-1/2) ≠ 0

• f(5) = 0

• f(-1/3) = 0

• f(1/2) = 0

Then, the correct option is: 5, − one third , one half.

Finally, the factorized form is: (x−5)(2x−1)(3x+1). If you expand it, you will get the original polynomial.