Question

If c(x) = 4x – 2 and d(x) = x2 + 5x, what is (cxd)(x)

Answer 1

Answer:
`(c*d)(x)=4x^3+18x^2-10x`

Explanation:

You know that the function
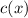`c(x)` and the function
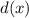`d(x)` are:

`c(x) = 4x - 2\\\\d(x) = x^2 + 5x`

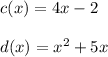
Then, in order to find
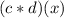`(c*d)(x)` you need to multiply the function
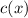`c(x)` by the function
`d(x)`:

`(c*d)(x)=(4x - 2)(x^2 + 5x)`

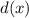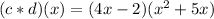
You must remember the Product of powers property, which states that:

`(a^m)(a^n)=a^((m+n))`

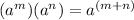
Now you can apply Distributive property:

`(c*d)(x)=4x^3+20x^2-2x^2-10x`

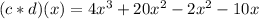
Finally, add the like terms. Then:

`(c*d)(x)=4x^3+18x^2-10x`

Answer 2

(cxd)(x) = 4x^3 + 18x^2 - 10x

Explanation:

We have two functions:

c(x) = 4x – 2

d(x) = x2 + 5x

And we need to find (cxd)(x) which is the multiplication of both functions:

(cxd)(x) = (4x – 2)(x^2 + 5x) = 4x × x^2 + 20x^2 - 2x^2 -10x

= 4x^3 + 18x^2 - 10x

Then: (cxd)(x) = 4x^3 + 18x^2 - 10x