Question

A jogger accelerates from rest to 4.86 m/s in 2.43 s. A car accelerates from 20.6 to 32.7 m/s also in 2.43 s. (a) Find the magnitude of the acceleration of the jogger. (b) Determine the magnitude of the acceleration of the car. (c) How much further does the car travel than the jogger during the 2.43 s?

Answer 1

Step-by-step explanation:

It is given that,

Initially, the jogger is at rest u₁ = 0

He accelerates from rest to 4.86 m, v₁ = 4.86 m

Time, t₁ = 2.43 s

A car accelerates from u₂ = 20.6 to v₂ = 32.7 m/s in t₂ = 2.43 s

(a) Acceleration of the jogger :

`a=(v-u)/(t)`

`a=(4.86\ m/s-0)/(2.43\ s)`

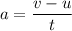
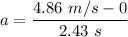
a₁ = 2 m/s²

(b) Acceleration of the car,

`a=(v-u)/(t)`

`a=(32.7\ m/s-20.6\ m/s)/(2.43\ s)`

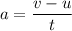
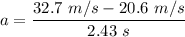
a₂ = 4.97 m/s²

(c) Distance covered by the car,

`d_1=u_1t_1+(1)/(2)a_1t_1^2`

`d_1=0+(1)/(2)* 2* (2.43)^2`

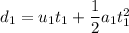
d₁ = 5.904 m

Distance covered by the jogger,

`d_2=u_2t_2+(1)/(2)a_2t_2^2`

`d_2=20.6* 2.43+(1)/(2)* 4.97* (2.43)^2`

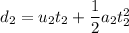
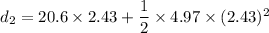
d₂ = 64.73 m

The car further travel a distance of, d = 64.73 m - 5.904 m = 58.826 m

Hence, this is the required solution.