Answer:
The triangles are congruent
Explanation:
Given
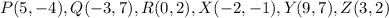
Required
Determine if PQR = XYZ
To do this, we make use of distance formula.
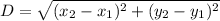
For PQ:
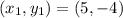 and
and
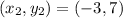
So:
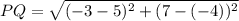
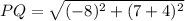
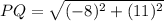
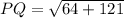
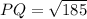
For XY:
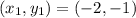
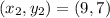
So:
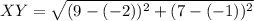
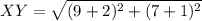
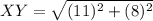
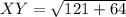
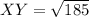
For QR:
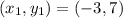 and
and
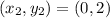
So:
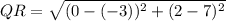
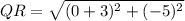
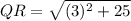
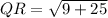
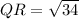
For YZ:
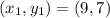 and
and
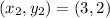
So:
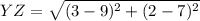
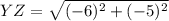
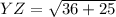
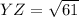
For PR:
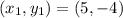 and
and
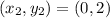
So:
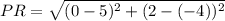
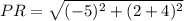
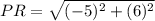
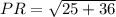
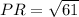
For XZ:
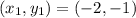 and
and
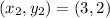
So:
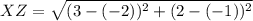
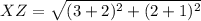
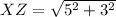
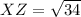
From the calculations above:
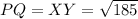
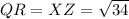
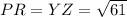
Hence, the triangles are congruent base on SSS (Sides- Sides-Sides)