Question

Which of the following is the correct equation for this function?

A. y= (x+4)(x+2)
B. y=x^2+ 3x – 2
C. y+ 2 = – 2(x+3)^2
D. y+ 2 = 2(x+3)^2

Answer 1

D. y + 2 = 2(x+3)^2

Explanation:

Answer 2

The equation which is correct for the given function is:

D.
`y+2=2(x+3)^2`

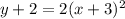
Explanation:

By looking at the graph we observe that the graph of the function passes through the point (-4,0) , (-2,0) , (-3,-2)

A)

`y=(x+4)(x+2)`

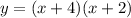
when x= -3 we have:

`y=(-3+4)(-3+2)\\\\y=1* (-1)\\\\y=-1\\eq -2`

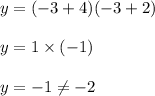
Hence, option: A is incorrect.

B)

`y=x^2+3x-2`

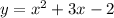
when x= -2 we have:

`y=(-2)^2+3* (-2)-2\\\\y=4-6-2\\\\y=-4\\eq 0`

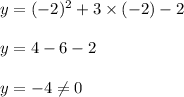
Hence, option: B is incorrect.

C)

`y+2=-2(x+3)^2`

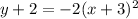
when x= -2 we have:

`y+2=-2(-2+3)^2\\\\y+2=-2`

`y=-4\\eq 0`

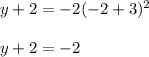
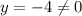
Hence, option: C is incorrect.

D)

`y+2=2(x+3)^2`

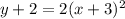
We see that the graph of this equation matches the given graph of the function.