Answer:
No Real roots to this Quadratic Equation
Explanation:
Our Quadratic equation is given as
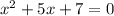
In order to find that do we have the real roots of a quadratic equation , the Discriminant must be greater or equal to 0. The Discriminant is denoted by D and given by the formula
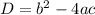
Where b is the coefficient of the middle term containing x, a is the coefficient of the term containing
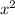 and the c is the constant term.
and the c is the constant term.
Hence we have
a = 1 , b = 5 and c = 7
Calculate D
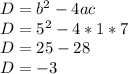
Hence we see that the Discriminant (D) is less than 0, our answer is no real roots to this quadratic equation.