Answer:
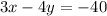
Explanation:
The standard form of a linear equation is
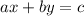 .
.
The given line has equation:
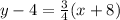
This is the point-slope form of the given line.
To find the standard form, we clear the fraction
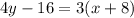
We expand the parenthesis now to get:
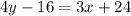
We group the variables on the LHS and the constants on the RHS.
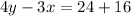
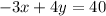
Multiply through by -1
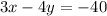
This is of the form:
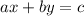 .
.