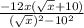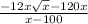Question

Rationalize the denominator- 12x/√x-10

Answer 1

`( - 12x √(x) - 120x)/( x - 100)`

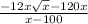
Step-by-step explanation

The given function is

`( - 12x)/( √(x) - 10 )`

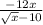
In the denominator we have

`√(x) - 10`

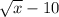
The conjugate of this surd is

`√(x) + 10`

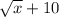
To rationalize this function, we multiply both the numerator and the denominator by the conjugate surd.

`( - 12x (√(x) + 10))/( (√(x) - 10)(√(x) + 1))`

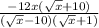
We apply the identity

`(a + b)(a - b) = {a}^(2) - {b}^(2)`

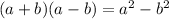
in the denominator.

This implies that,

`\frac{ - 12x (√(x) + 10)}{ (√(x))^(2) - {10}^(2) }`

`( - 12x √(x) - 120x)/( x - 100)`