Answer:
120°.
Explanation:
The sum of all interior angles in a polygon with
 sides (
sides (
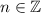 ,
,
 ) is equal to
) is equal to
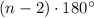 . (Credit: Mathsisfun.)
. (Credit: Mathsisfun.)
The polygon here has 6 sides.
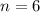 . Its interior angles shall add up to
. Its interior angles shall add up to
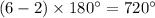 .
.
Consider the properties of a regular polygon. (Credit: Mathsisfun.)
- All sides in a regular polygon are equal in length.
- All angles in a regular polygon are also equal.
There are six interior angles in a polygon with 6 sides. All six of them are equal. Thus, each of the six interior angle will be
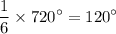 .
.