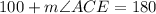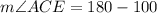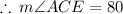ANSWER
Step-by-step explanation
Recall that adjacent angles on a straight line will add up to 180°
From the diagram, m<ACD and m<ACE are adjacent angles on a straight line because they have a common vertex at C.
We sum the two angles and equate them to 180°
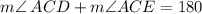
From the diagram
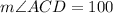
We substitute the known angle to obtain: