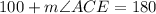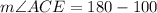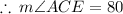Question

If m Subject geometry
Angle pairs

Answer 1

the angles are supplementary meaning they equal 180 degrees so 100-x=180

x=80

Answer 2

`m \angle ACE = 80 \degree`

Step-by-step explanation

Recall that adjacent angles on a straight line will add up to 180°

From the diagram, m<ACD and m<ACE are adjacent angles on a straight line because they have a common vertex at C.

We sum the two angles and equate them to 180°

`m \angle \: ACD + m \angle ACE = 180 \degree`

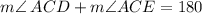
From the diagram

`m\angle ACD= 100 \degree`

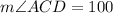
We substitute the known angle to obtain:

`100 \degree + m \angle ACE = 180 \degree`

`m \angle ACE = 180 \degree - 100 \degree`

`\therefore \: m \angle ACE = 80 \degree`