Question

Given sin28.4=.4756, cos28.4=.8796, and tan28.4=.5407 find the cot of 61.6

Answer 1

The cotangent of 61.6° is .5407.

Explanation:

Refer to the sketch attached.

61.6° + 28.4° = 90°. In other words, 61.6° is the complementary angle of 28.4°.

Consider a right triangle OAB with a 61.6° angle
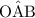`\rm O\hat{A}B`. The other acute angle
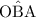`\rm O\hat{B}A` will be 28.4°.

`\displaystyle \tan{61.6\textdegree{}}=\tan{\rm O\hat{A}B} = \frac{\text{Opposite of }\rm O\hat{A}B}{\text{Adjacent of }\rm O\hat{A}B} = (a)/(b)`.

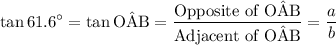The cotangent of an angle is the reciprocal of its tangent.

`\displaystyle \cot{61.6^(\circ)}=\frac{1}{\tan{\rm O\hat{B}A}} = \frac{\text{Adjacent of }\rm O\hat{B}A}{\text{Opposite of }\rm O\hat{B}A} = (a)/(b) = \tan{\rm O\hat{A}B} = \tan{28.4^(\circ)}`.

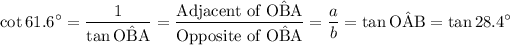In other words,

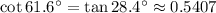`\cot{61.6^(\circ)} = \tan{28.4^(\circ)} \approx 0.5407`.