Answer:
720
Explanation:
Given : The word ABSENT
To Find: How many different 6-letter arrangements can be formed using the letters in the word ABSENT, if each letter is used only once?
Solution:
Number of letters in ABSENT = 6
So, No. of arrangements can be formed using the letters in the word ABSENT, if each letter is used only once = 6!
=

=
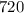
So, Option C is true
Hence there are 720 different 6-letter arrangements can be formed using the letters in the word ABSENT.