Question

Consider this expression and the steps to evaluate it.

4^5(−2)^9/4^8(−2)^3
1. Apply the quotient of powers:     (−2)^a/4^b

2. Evaluate powers:          c/d

Select the value of each variable.
a = _
b = _
c = _
d = _

Answer 1

a=6

b=3

c=64

d=64

Explanation:

Answer 2

value of a = 6

value of b = 3

value of c = 64

value of d= 64

Explanation:

1. Apply the quotient of powers:

(-2)^a / 4^b

In the given expression:

`4^5(-2)^9/4^8(-2)^3`

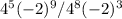
We know if we have the same base then the powers are subtracting if the bases are in numerator and denominator

i.e
`a^m/a^n = a^(m-n)`

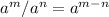
Solving:

`=(-2)^(9-3)/4^(-5+8)\\=(-2)^6/4^3`

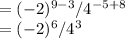
So, the value of a = 6

and the value of b = 3

2. Evaluate Powers

c/d

We have

`(-2)^6/4^3`

Solving:

When power is even negative sign changes into plus sign

64/64

So value of c = 64

and value of d= 64