Question

Which of the following shows the graph of y=2e^x?

Answer 1

For this case we must indicate the graph corresponding to the following equation:

`y = 2e ^ x`

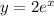
Then, we evaluate the equation for
`x = 0`

`y = 2e ^ 0`

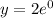
We have by definition, any number raised to zero results in 1.

So:

`y = 2`

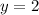
Now we evaluate the equation for x = -1

`y = 2e ^ {-1}\\y = \frac {2} {e}\\y = 0.736`

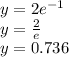
We already have two points to graph:

`(0,2)\\(-1,0.736)`

Observing the options, we realize that the correct option is option C.

It should be noted that graphs A and D, by definition, do not correspond to the exponential function.

Answer:

Option C

Answer 2

The third one.

Explanation:

When x=0, the function y=2e^x equals:

y=2e^x = 2e^(0) = 2.

For that reason, the graph should cross the y-axis at the point (0, 2). The only graph that meets this requirement is the third one :).