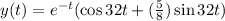Question

Y" +2y' +17y=0; y(0)=3, y'(0)=17

Answer 1

The solution is
`y(t)=e^(-t)(\cos 32t + ((5)/(8)) \sin 32t)`

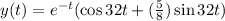
Explanation:

We need to find the solution of
`y''+2y'+17y=0` with

condition
`y(0)=3,\ y'(0)=17`

This is a homogeneous equation with characteristic polynomial

`r^(2)+2r+17=0`

using quadratic formula
`x=\frac{-b\pm \sqrt{b^(2)-4ac}}{2a}`

`r=\frac{-2\pm \sqrt{2^(2)-4(1)(17)}}{2(1)}`

`r=(-2\pm √(4-68))/(2)`

`r=(-2\pm √(-64))/(2)`

`r=(-2\pm 64i)/(2)`

`r=-1 \pm 32i`

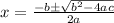
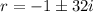
The general solution for eigen value
`a \pm ib` is

`y(t)=e^(at)(A \cos bt + B \sin bt)`

`y(t)=e^(-t)(A \cos 32t + B \sin 32t)`

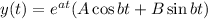
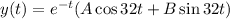
Differentiate above with respect to 't'

`y'(t)=-e^(-t)(A \cos 32t + B \sin 32t) + e^(-t)(-32A \sin 32t + 32B \cos 32t)`

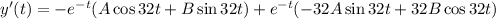
Since, y(0)=3

`y(0)=e^(0)(A \cos(0) + B \sin(0))`

`3=(A \cos(0) +0)`

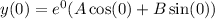
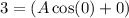
so, A=1

Since, y'(0)=17

`y'(0)=-e^(0)(3 \cos(0) + B \sin(0)) + e^(0)(-32(3) \sin(0) + 32B \cos (0))`

`17=-(3 \cos(0)) + (0 + 32B \cos (0))`

`17=-3 + 32B`

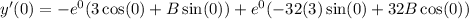
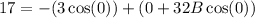
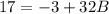
add both the sides by 3,

`17+3 = 32B`

`20= 32B`

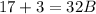
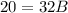
divide both the sides, by 32,

`(20)/(32)= B`

`(5)/(8)= B`

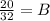
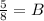
Put the value of constants in
`y(t)=e^(-t)(A \cos 32t + B \sin 32t)`

`y(t)=e^(-t)((1) \cos 32t + ((5)/(8)) \sin 32t)`

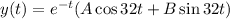
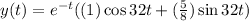
Therefore, the solution is
`y(t)=e^(-t)(\cos 32t + ((5)/(8)) \sin 32t)`