Find the area under the curve y =f( x) on [a,b] given f(x)=tan(3x) where a=0 b=pi/12

Question

asked May 27, 2020 160k views

1 Answer

Olotiar · Answer 1 · 2020-06-01T05:35:31+0000

Answer:

The area under the curve y=f(x) on [a,b] is
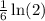$(1)/(6)\ln(2)$ square units.

Explanation:

The given function is

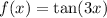
$f(x)=\tan(3x)$

where a=0 and b=pi/12.

The area under the curve y=f(x) on [a,b] is defined as

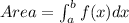
$Area=\int_(a)^(b)f(x)dx$

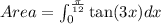
$Area=\int_(0)^{(\pi)/(12)}\tan (3x)dx$

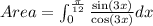
$Area=\int_(0)^{(\pi)/(12)}(\sin (3x))/(\cos (3x))dx$

Substitute cos (3x)=t, so

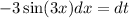
$-3\sin (3x)dx=dt$

$\sin (3x)dx=-(1)/(3)dt$

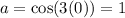
$a=\cos (3(0))=1$

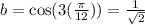
$b=\cos (3((\pi)/(12)))=(1)/(√(2))$

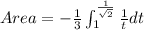
$Area=-(1)/(3)\int_(1)^{(1)/(√(2))}(1)/(t)dt$

$Area=-(1)/(3)[\ln t]_(1)^{(1)/(√(2))$

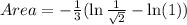
$Area=-(1)/(3)(\ln (1)/(√(2))-\ln (1))$

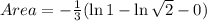
$Area=-(1)/(3)(\ln 1-\ln √(2)-0)$

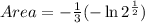
$Area=-(1)/(3)(-\ln 2^{(1)/(2)})$

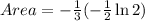
$Area=-(1)/(3)(-(1)/(2)\ln 2)$

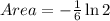
$Area=-(1)/(6)\ln 2$

Therefore the area under the curve y=f(x) on [a,b] is
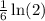$(1)/(6)\ln(2)$ square units.