Answer:
The distance is 4.726
Explanation:
we need to find the distance from the point to the line
Given:- point (-1,-2,1) and line ; x=4+4t, y=3+t, z=6-t .
used formula
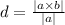
Let point P be (-1,-2,1)
using value t=0 and t=1
The point Q (4 , 3, 6) and R ( 8, 4, 5)
Let a be the vector from Q to R : a = < 8 - 4, 4 - 3, 5 - 6 > = < 4, 1, -1 >
Let b be the vector from Q to P: b = < -1 - 4, -2 - 3, 1 - 6> = < -5, -5, -5 >
The cross product of a and b is:
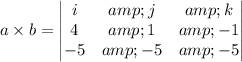
= -6i+15j-15k
The distance is :
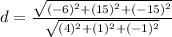


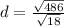
≈4.726
Therefore, the distance is 4.726