Question

What are the solutions of the equation x4 + 6x2 + 5 = 0? Use u substitution to solve.

Answer 1

2nd answer.

Explanation:

see attached.

Answer 2

Answer with Step-by-step explanation:

We have to find the solution of the equation:

`x^4+6x^2+5=0`

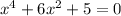
Let u=x²

Then, above equation is transformed to:

`u^2+6u+5=0`

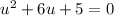
it could also be written as:

`u^2+5u+u+5=0`

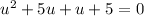
u(u+5)+1(u+5)=0

(u+1)(u+5)=0

either u+1=0 or u+5=0

either u= -1 or u= -5

Putting u=x²

x² = -1 or x² = -5

On taking square root both sides

x= ± i or x= ± i√5

Hence, roots of the equation
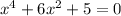`x^4+6x^2+5=0` are:

i , -i , i√5 and -i√5