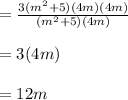Answer:
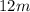
Explanation:
Given the expression
 , we can rewrite it in this form:
, we can rewrite it in this form:

Now we must multiply the numerator of the first fraction by the numerator of the second fraction and the denominator of the first fraction by the denominator of the second fraction:
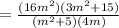
According to the Quotient of powers property:
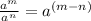
And the Product of powers property states that:
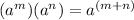
Then, simplifying, we get: