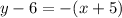2 Answers

Rupsingh · Answer 1 · 2020-03-04T22:20:18+0000

For this case we have by definition, that the equation of a line in the point-slope form is given by:

$(y-y_ {0}) = m (x-x_ {0})$

Where:

m: It's the slope

$(x_ {0}, y_ {0}):$ It is a point through which the line passes.

$m = \frac {y2-y1} {x2-x1}$

We have as data two points, replacing:

$m = \frac {1-6} {0 - (- 5)}\\m = \frac {1-6} {0 + 5}\\m = \frac {-5} {5}\\m = -1$

We substitute a point, then the equation is:

$(y-1) = - 1 (x-0)\\(y-1) = - x$

Answer:

Leacroft · Answer 2 · 2020-03-08T12:21:54+0000

Answer:
y-6=-(x+5)

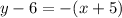
Explanation:

The Point-slope form of the equation of the line is:

y-y_1=m(x-x_1)

Where "m" is the slope of the line and
(x_1,y_1) is a point on the line.

We know that this line passing through the points (-5,6) and (0,1), then we can find the slope with this formula:

m=(y_2-y_1)/(x_2-x_1)

Substituting, we get:

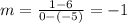
m=(1-6)/(0-(-5))=-1

Finally, we can substitute the point (-5,6) and the slope into
y-y_1=m(x-x_1) , then:

y-6=-(x-(-5))

y-6=-(x+5)

Please log in or register to add a comment.