Answer:
The correct option is C.
Explanation:
The standard form of a parabola is

The table of values represents the coordinate pairs of the parabola. It means the graph of the parabola must be passes through these coordinate pairs.
From the given table it is clear that the parabola passes through the points (0.5,21), (1,34) and (1.5,39).
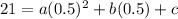
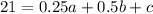 .... (1)
.... (1)

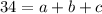 .... (2)
.... (2)
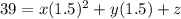
 .... (3)
.... (3)
On solving (1), (2) and (3), we get
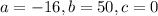
The equation of parabola is

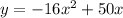
The graph of parabola is shown below. It is same as graph in option C.
Therefore the correct option is C.