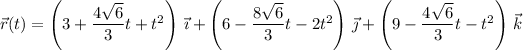Question

At time t=0, a particle is located at the point (3,6,9). It travels in a straight line to the point (5,2,7), has speed 8 at (3,6,9) and constant acceleration 2i−4j−2k. Find an equation for the position vector of the particle.

Answer 1

To find the equation for the position vector of the particle, use the formula r(t) = r(0) + v(0) * t + (1/2) * a * t^2.

Step-by-step explanation:

To find the equation for the position vector of the particle, use the following steps:

1. Write down the initial position vector, r(0), which is (3,6,9).
2. Use the formula for the position vector of a particle with constant acceleration, r(t) = r(0) + v(0) * t + (1/2) * a * t^2, where r(t) is the position vector at time t, v(0) is the initial velocity vector, and a is the constant acceleration vector.
3. Substitute the values into the formula and simplify to get the equation for the position vector.

For the given problem, the equation for the position vector of the particle is: r(t) = (3 + 4t)i + (6 - 4t + 2t^2)j + (9 - 2t + t^2)k.

Answer 2

The particle has constant acceleration according to

`\vec a(t)=2\,\vec\imath-4\,\vec\jmath-2\,\vec k`

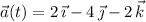
Its velocity at time
`t` is

`\displaystyle\vec v(t)=\vec v(0)+\int_0^t\vec a(u)\,\mathrm du`

`\vec v(t)=\vec v(0)+(2\,\vec\imath-4\,\vec\jmath-2\,\vec k)t`

`\vec v(t)=(v_(0x)+2t)\,\vec\imath+(v_(0y)-4t)\,\vec\jmath+(v_(0z)-2t)\,\vec k`

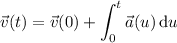
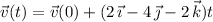
Then the particle has position at time
`t` according to

`\displaystyle\vec r(t)=\vec r(0)+\int_0^t\vec v(u)\,\mathrm du`

`\vec r(t)=(3+v_(0x)t+t^2)\,\vec\imath+(6+v_(0y)t-2t^2)\,\vec\jmath+(9+v_(0z)t-t^2)\,\vec k`

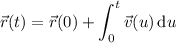
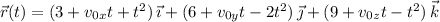
At at the point (3, 6, 9), i.e. when
`t=0`, it has speed 8, so that

`\|\vec v(0)\|=8\iff{v_(0x)}^2+{v_(0y)}^2+{v_(0z)}^2=64`

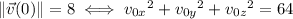
We know that at some time
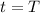`t=T`, the particle is at the point (5, 2, 7), which tells us

`\begin{cases}3+v_(0x)T+T^2=5\\6+v_(0y)T-2T^2=2\\9+v_(0z)T-T^2=7\end{cases}\implies\begin{cases}v_(0x)=\frac{2-T^2}T\\\\v_(0y)=\frac{2T^2-4}T\\\\v_(0z)=\frac{T^2-2}T\end{cases}`

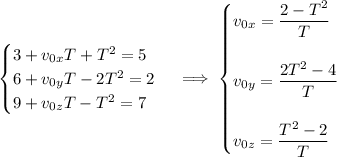
and in particular we see that

`v_(0y)=-2v_(0x)`

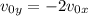
and

`v_(0z)=-v_(0x)`

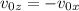
Then

`{v_(0x)}^2+(-2v_(0x))^2+(-v_(0x))^2=6{v_(0x)}^2=64\implies v_(0x)=\pm\frac{4\sqrt6}3`

`\implies v_(0y)=\mp\frac{8\sqrt6}3`

`\implies v_(0z)=\mp\frac{4\sqrt6}3`

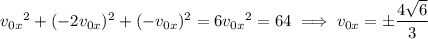
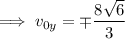
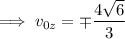
That is, there are two possible initial velocities for which the particle can travel between (3, 6, 9) and (5, 2, 7) with the given acceleration vector and given that it starts with a speed of 8. Then there are two possible solutions for its position vector; one of them is

`\vec r(t)=\left(3+\frac{4\sqrt6}3t+t^2\right)\,\vec\imath+\left(6-\frac{8\sqrt6}3t-2t^2\right)\,\vec\jmath+\left(9-\frac{4\sqrt6}3t-t^2\right)\,\vec k`