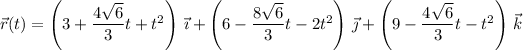The particle has constant acceleration according to
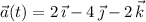
Its velocity at time
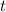 is
is
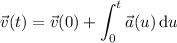
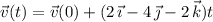
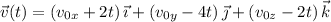
Then the particle has position at time
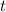 according to
according to
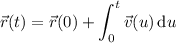
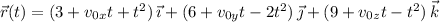
At at the point (3, 6, 9), i.e. when
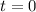 , it has speed 8, so that
, it has speed 8, so that
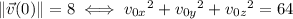
We know that at some time
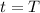 , the particle is at the point (5, 2, 7), which tells us
, the particle is at the point (5, 2, 7), which tells us
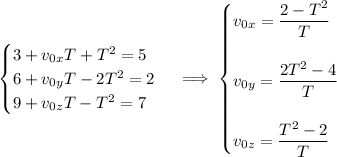
and in particular we see that
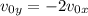
and
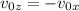
Then
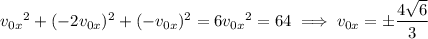
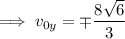
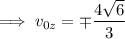
That is, there are two possible initial velocities for which the particle can travel between (3, 6, 9) and (5, 2, 7) with the given acceleration vector and given that it starts with a speed of 8. Then there are two possible solutions for its position vector; one of them is