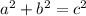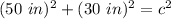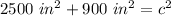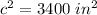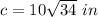Question

I have like no idea how to do any of this please help!

Answer 1

59.03 deg

58.31 in

Explanation:

The wall and the floor form a right angle. The parts of the wall and the floor from the corner until they intersect the ladder are the legs of a right angle. The ladder is the hypotenuse of the right angle.

You can use trigonometry to find the measure of the angle.

For the angle where the ladder touches the floor, the leg along the wall is the opposite leg, and the leg along the floor is the adjacent leg.

Use the tangent ratio.

`\tan A = (opp)/(adj)`

`\tan A = (50)/(30) = (5)/(3)`

`A = \tan^(-1) (5)/(3)`

`A = 59.03^\circ`

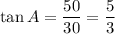
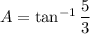
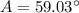
To find the length of the ladder, which is the hypotenuse of the triangle, you can use trigonometry again or the Pythagorean Theorem.

I'll use the Pythagorean Theorem.

`a^2 + b^2 = c^2`

`(50~in)^2 + (30~in)^2 = c^2`

`2500~in^2 + 900~in^2 = c^2`

`c^2 = 3400~in^2`

`c = √(3400~in^2)`

`c = 10√(34)~in`

`c \approx 58.31~in`

Answer 2

Tan(angle) = Opposite leg / Adjacent leg

Tan (Angle) = 50/30

Angle = arctan(50/30)

Angle = 59.0 degrees.

Find the length of the ladder using the Pythagorean theorem:

50^2 + 30^2 = X^2

2500 + 900 = x^2

x^2 = 3400

x = √3400

x = 58.3 inches.