Question

Find the inverse of the given function. f(x)= -1/2SQR x+3, x greater than or equal to -3

Answer 1

So, the inverse of function

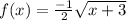`f(x) = (-1)/(2) √(x+3)` is
`f^(-1)(x)= 4x^2-3`

Explanation:

We need to find the inverse of the given function

`f(x) = (-1)/(2) √(x+3)`

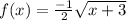
To find the inverse we replace f(x) with y

`y = (-1)/(2) √(x+3)`

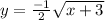
Now, replacing x with y and y with x

`x = (-1)/(2) √(y+3)`

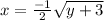
Now, we will find the value of y in the above equation

Multiplying both sides by -2

`-2x = √(y+3)`

Taking square on both sides

`(-2x)^2 = (√(y+3))^2`

`4x^2 = y+3`

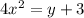
Finding value of y

`y = 4x^2-3`

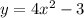
Replacing y with f⁻¹(x)

`f⁻¹(x)= 4x^2-3`

So, the inverse of function

`f(x) = (-1)/(2) √(x+3)` is
`f^(-1)(x)= 4x^2-3`

Answer 2

`f^( - 1) (x) =4 {x}^(2)- 3`

EXPLANATION

A function will have an inverse if and only if it is a one-to-one function.

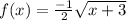The given function is

`f(x) = - (1)/(2) √(x + 3) \: \: where \: \: x \geqslant - 3`

To find the inverse of this function, we let

`y=- (1)/(2) √(x + 3)`

Next, we interchange x and y to get,

`x=- (1)/(2) √(y+ 3)`

We now solve for y.

We must clear the fraction by multiplying through with -2 to get;

`- 2x = √(y + 3)`

Square both sides of the equation to get:

`(- 2x)^(2) = (√(y+ 3)) ^(2)`

`4x^(2) = y + 3`

Add -3 to both sides

`4 {x}^(2) - 3 = y`

Or

`y = 4 {x}^(2)- 3`

This implies that,

`f^( - 1) (x) =4 {x}^(2)- 3`

This is valid if and only if

`x \geqslant - 3`