Answer:
The turning point is (-2,10)
Explanation:
we have
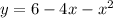
This is a quadratic equation (vertical parabola) open downward
we know that
The turning point of a quadratic equation is the vertex
so
Convert the quadratic equation into vertex form
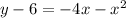
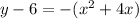
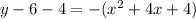
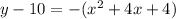
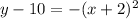
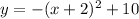 ----> equation in vertex form
----> equation in vertex form
The vertex is the point (-2,10)
therefore
The turning point is (-2,10)