Question

Find the perimeter of each of the two noncongruent triangles where a = 15, b = 20, and A = 29°

Answer 1

b on edge

Explanation:

Answer 2

Answer with explanation:

Using Sine Rule for Congruence of Triangles

`\Rightarrow(a)/(\ SinA)=(b)/(\ Sin B)=(c)/(\ Sin C)\\\\\Rightarrow(15)/(\ Sin29^(\circ))=(20)/(\ Sin B)\\\\\Rightarrow(15)/(0.49)=(20)/(\ Sin B)\\\\\Rightarrow \ SinB=(20 * 0.49)/(15)\\\\\Rightarrow \ SinB=(9.8)/(15)\\\\\Rightarrow \ SinB=0.65\\\\B=41^(\circ)`

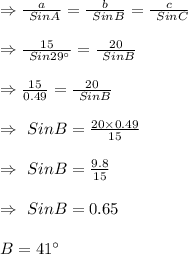
Using Angle Sum Property of Triangle

⇒∠A+∠B+∠C=180°

⇒29°+41°+∠C=180°

⇒∠C=180°-70°

⇒∠C=110°

→Again Using Sine Rule

`\Rightarrow (b)/(\ Sin B)=(c)/(\ Sin C)\\\\\Rightarrow (20)/(\ Sin 41^(\circ))=(c)/(\ Sin 110^(\circ))\\\\\Rightarrow (20)/(0.65)=(c)/(0.94)\\\\\Rightarrow (20 * 0.94)/(0.65)=c\\\\\Rightarrow c=(18.8)/(0.65)\\\\\Rightarrow c=28.92`

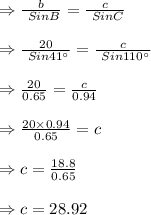
Length of third Side =28.92 unit

So,Perimeter of Triangle

=Sum of sides of triangle

=a +b +c

=15 + 20 +28.92

= 63.92 unit