Question

How many solutions are possible for a triangle with A = 113° , a = 15, and b = 8

Answer 1

b on edge

Explanation:

Answer 2

One solution.

Explanation:

To determine the number of possible solutions for a triangle with A = 113° , a = 15, and b = 8, we're going to use the law of sines which states that: "When we divide side a by the sine of angle A it is equal to side b divided by the sine of angle B, and also equal to side c divided by the sine of angle C".

Using the law of sines we have:

`(sin(A))/(a) = (sin(B))/(b)`

`(sin(113))/(15) = (sin(B))/(8)`

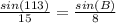
Solving for B, we have:

`sin(B)=0.4909`

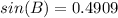
∠B = 29.4°

Therefore, the measure of the third angle is: ∠C = 37.6°

There is another angle whose sine is 0.4909 which is 180° - 29.4° = 150.6 degrees. Given that the sum of all three angles of any triangle must be equal to 180 deg, we can't have a triangle with angle B=113° and C=150.6°, because B+C>180.

Therefore, there is one triangle that satisfies the conditions.