Question

PATH INDEPENDENCE? 13-19 from Check, and if independent, integrate from (0, 0, 0) to (a, b, c) 13. 2e (x cos 2y dx - sin 2y dy)

Answer 1

The integral is path-independent if there is a scalar function
`f` whose gradient is

`\\abla f=(2e^x\cos2y,-\sin2y)`

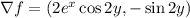
(at least, that's what it looks like the given integrand is)

Then

`(\partial f)/(\partial x)=2e^x\cos 2y\implies f(x,y)=2e^x\cos2y+g(y)`

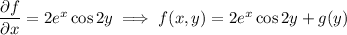
Differentiating both sides with respect to
`y` gives

`(\partial f)/(\partial y)=-4e^x\sin 2y\\eq-\sin2y`

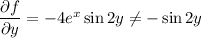
so the line integral *is* dependent on the path. (again, assuming what I've written above actually reflects what the question is asking)