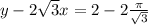Question

Find an equation of the tangent line to the curve at the given point. y=secx, (pi/3, 2)

Answer 1

Equation of tangent is
`y-2√(3)x=2-2(\pi)/(√(3))`

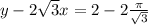
Explanation:

Given:

Equation of curve, y = sec x

Passing through point =
`((\pi)/(3),2)`

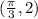
We need to find Equation of tangent to the given curve and at the given point.

First we find the slope of the tangent by differentiating the given curve.

As we know that slope of the tangent, m =
`\frac{\mathrm{d}y}{\mathrm{d} x}`

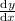
So, consider

y = sec x

`\frac{\mathrm{d}y}{\mathrm{d} x}=\frac{\mathrm{d}(sec\,x)}{\mathrm{d} x}`

`\frac{\mathrm{d}y}{\mathrm{d} x}=sec\,x\:tan\,x`

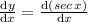
Now we find value of slope at given point,

put x =
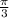`(\pi)/(3)` in above derivate

we get

`\frac{\mathrm{d}y}{\mathrm{d} x}=sec\,(\pi)/(3)\:tan\,{\pi}{3}=2√(3)`

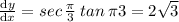
Now using Slope point form, we have

Equation of tangent

`y-y_1=m(x-x_1)`

`y-2=2√(3)(x-(\pi)/(3))`

`y=2√(3)x-2√(3)(\pi)/(3)+2`

`y-2√(3)x=2-2(\pi)/(√(3))`

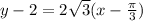
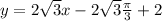
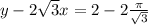
Therefore, Equation of tangent is
`y-2√(3)x=2-2(\pi)/(√(3))`