Question

The coordinates G(7,3), H(9, 0), (5, -1) form what type of polygon?

an obtuse triangle
an acute triangle
O an equilateral triangle
a right triangle

Answer 1

ACUTE !!!!!!!!

Explanation:

Answer 2

Is an acute triangle

Explanation:

we know that

the formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

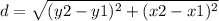
we have

G(7,3), H(9, 0), I(5, -1)

step 1

Find the distance GH

substitute in the formula

`d=\sqrt{(0-3)^(2)+(9-7)^(2)}`

`d=\sqrt{(-3)^(2)+(2)^(2)}`

`GH=√(13)\ units`

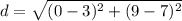
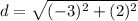
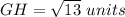
step 2

Find the distance IH

substitute in the formula

`d=\sqrt{(0+1)^(2)+(9-5)^(2)}`

`d=\sqrt{(1)^(2)+(4)^(2)}`

`IH=√(17)\ units`

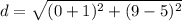
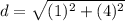
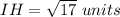
step 3

Find the distance GI

substitute in the formula

`d=\sqrt{(-1-3)^(2)+(5-7)^(2)}`

`d=\sqrt{(-4)^(2)+(-2)^(2)}`

`GI=√(20)\ units`

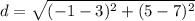
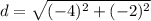
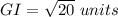
step 4

Verify what type of triangle is the polygon

we know that

If applying the Pythagoras Theorem

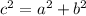`c^(2)=a^(2)+b^(2)` ----> is a right triangle

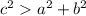`c^(2)> a^(2)+b^(2)` ----> is an obtuse triangle

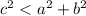`c^(2)< a^(2)+b^(2)` ----> is an acute triangle

where

c is the greater side

we have

`c=√(20)\ units`

`a=√(17)\ units`

`b=√(13)\ units`

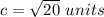
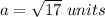
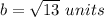
substitute

`c^(2)= (√(20))^(2)=20`

`a^(2)+b^(2)=(√(17))^(2)+(√(13))^(2)=30`

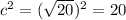
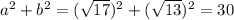
therefore

`c^(2)< a^(2)+b^(2)`

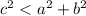
Is an acute triangle