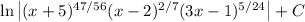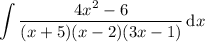
You have a rational expression whose numerator's degree is smaller than the denominator's. This tells you you should consider a partial fraction decomposition. We want to rewrite the integrand in the form
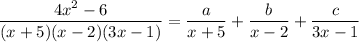

You can use the "cover-up" method here to easily solve for
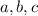 . It involves fixing a value of
. It involves fixing a value of
 to make 2 of the 3 terms on the right side disappear and leaving a simple algebraic equation to solve for the remaining one.
to make 2 of the 3 terms on the right side disappear and leaving a simple algebraic equation to solve for the remaining one.
- If
 , then
, then
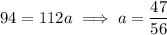
- If
 , then
, then

- If
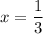 , then
, then
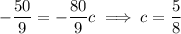
So the integral we want to compute is the same as
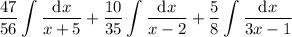
and each integral here is trivial. We end up with
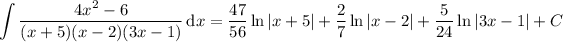
which can be condensed as