Answer:
The value of k is 6
Explanation:
we need to find the value of k
Given : -
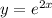 is the solution
is the solution
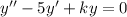
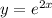 ........(1)
........(1)
differentiate
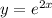 with respect to 'x'
with respect to 'x'
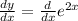
Since,
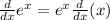
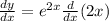
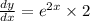
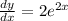
so,
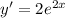 ..........(2)
..........(2)
Again differentiation above with respect to 'x'
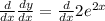
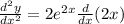
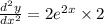
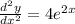
so,
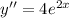 ........(3)
........(3)
Now, put the value of
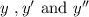 in
in
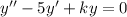
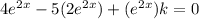
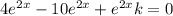
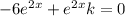
add both the sides by
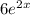
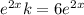
Cancel out the same terms from left and right sides
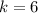
Hence, the value of k is 6