Answer:
B
Explanation:
The equation of a parabola in vertex form is
y = a(x - h)² + k
where (h, k) are the coordinates of the vertex and a is a multiplier
Given
y = (x + 3)² + (x + 4)² ← expand and simplify
= x² + 6x + 9 + x² + 8x + 16
= 2x² + 14x + 25
To obtain vertex form use the method of completing the square
The coefficient of the x² term must be 1
Factor out 2 from 2x² + 14x
y = 2(x² + 7x) + 25
add/ subtract ( half the coefficient of the x- term )² to x² + 7x
y = 2(x² + 2(
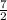 ) x +
) x +
 -
-
 ) + 25
) + 25
y = 2(x +
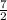 )² -
)² -
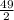 +
+
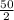
y = 2(x +
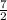 )² +
)² +
