Question

Find the equation in standard form , of the line passing through points (2,-3) and (4,2)

Answer 1

The form of linear equation that describes line is:

`y=sx+n`

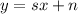
First we must calculate the slope.

`s=\frac{\Delta{y}}{\Delta{x}}=(2-(-3))/(4-2)=(5)/(2)`

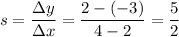
Now it looks a bit more like this:

`y=(5)/(2)x+n`

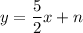
All we need now is to put in y and x from one point doesn't matter which. I'll pick A.

The equation now looks like this:

`-3=(5)/(2)\cdot2+n`

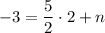
Solve for n.

`</p><p>-3=5+n \\</p><p>n=-8</p><p>`

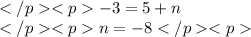
And finally write the equation.

`f(x)=(5)/(2)x-8`

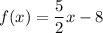
Hope this helps.

r3t40