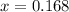Answer:
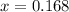
Explanation:
To solve the equation
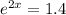 you need to apply natural logarithm to both sides of the equation:
you need to apply natural logarithm to both sides of the equation:
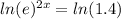
According to the logarithms property:
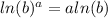
Then, applying the property, you get:
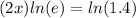
You need to remember the following:
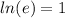
Therefore:
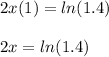
And finally, you must divide both sides of the equation by 2:
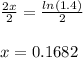
Rounded to the nearest thousand: